Teori Kebahagiaan menurut Einhorn

 Jangan memikirkan semua hal yang Anda inginkan yang tidak Anda miliki. Pikirkan semua hal yang tidak Anda inginkan yang tidak Anda miliki. – Kebijaksanaan kue keberuntungan

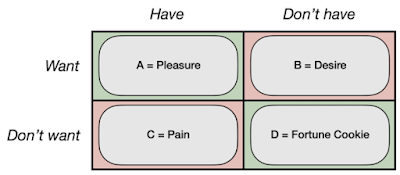
Hillel Einhorn, salah satu bapak baptis teori keputusan perilaku (lihat Hogarth & Klayman, 1988, untuk obituari yang penuh kasih), pernah menemukan potongan kebijaksanaan epigrafis ini dalam kue keberuntungan, yang membuatnya berpikir tentang hal-hal yang tidak dia inginkan dan lakukan. tidak memiliki (lihat di sini). Einhorn melihat sekilas teori statistik kebahagiaan. Setelah kita membedakan, katanya, hal-hal yang kita inginkan dari hal-hal yang tidak kita inginkan dan hal-hal yang kita miliki dari hal-hal yang tidak kita miliki, kita dapat melihat tabel frekuensi 2 kali 2. Mari kita sebut hal-hal yang kita inginkan dan miliki A, hal-hal yang kita inginkan dan tidak miliki B, hal-hal yang tidak kita inginkan dan miliki C, dan hal-hal yang tidak kita inginkan atau miliki D. Sekarang kita dapat memperkirakan korelasi antara ( tidak) menginginkan dan (tidak) memiliki. Korelasi positif akan menunjukkan kebahagiaan.

Sebut saja konjungsi keinginan dan kesenangan (sel A, di kiri atas matriks pada gambar). Konjungsi keinginan dan tidak-memiliki, yaitu, sel B, dapat disebut keinginan, dan secara khusus keinginan yang tidak terpenuhi. Konjungsi tidak-keinginan dan kaya, sel C, bisa disebut rasa sakit. Akhirnya, sel kue keberuntungan Einhorn, D, adalah gabungan dari tidak-ingin dan tidak-memiliki.’ Dalam matriks, sel A dan D diarsir hijau untuk menunjukkan nilai positif, sedangkan sel B dan C diarsir merah muda untuk nilai negatif. Korelasi antara baris dan kolom adalah = (AD-BC) / (A+B)(C+D)(A+C)(B+D).

Mari kita masukkan beberapa angka ke dalam sel untuk melihat bagaimana koefisien berperilaku dan pelajaran apa yang bisa diajarkan tentang kebahagiaan. Ada beberapa kalkulator yang tersedia secara online. Untuk penjelajahan ini, mari kita gunakan situs Statology. Kami mulai dengan menghasilkan angka menggunakan dua asumsi sederhana. Pertama, anggaplah segala sesuatunya berjalan dengan baik karena ada banyak kesenangan yang muncul dalam pikiran tetapi sedikit keinginan atau rasa sakit. Kedua, acara kue keberuntungan Einhorn, karena itu bukan acara, sulit untuk dipikirkan. Mengambil A = 10, B = 5, C = 5, dan D = 0 sebagai permulaan, kita menemukan bahwa = -.333. Ini adalah hasil yang tidak menyenangkan, meskipun ada banyak kesenangan karena ada keinginan yang tidak terpenuhi dan rasa sakit yang digabungkan. Kita bahkan mungkin menghitung berkah kita dan mendapatkan jumlah kesenangan hingga 100. Korelasinya berkurang kekuatannya, tetapi tetap negatif dengan = -.048. Tidak ada jumlah kesenangan positif yang menghasilkan korelasi positif jika tiga angka lainnya tetap sama. Namun, memasukkan Einhorn hanya dengan 3 instance di sel D, mengubah korelasi menjadi = 0,04 positif. Ketika, seperti yang masuk akal untuk diasumsikan, beberapa non-peristiwa yang tidak diinginkan segera muncul dalam pikiran, hanya dengan memikirkan beberapa non-peristiwa seperti itu memiliki efek bermanfaat yang lebih kuat pada asosiasi keseluruhan daripada menambahkan lebih banyak berkah kepada mereka yang sudah dihitung.

Kita mungkin bertanya-tanya apakah koefisien mewakili realitas psikologis. Seorang skeptis mungkin berpendapat bahwa tidak ada yang lain selain keadaan psikologis sementara. Saat kita memikirkan salah satu dari 4 sel dalam skema kita, kita mewakili kesenangan atau rasa sakit, keinginan yang tidak terpenuhi, atau kemalangan yang lolos, dan kita merasakannya. Versi radikal dari argumen ini adalah bahwa kita tidak dapat mengintegrasikan keadaan ini atau menggabungkannya karena hasilnya tidak akan sesuai dengan keadaan pengalaman apa pun. Bentuk skeptisisme yang lebih memaafkan mengatakan kita dapat menjumlahkan entri positif (A + D) dan mengurangi entri negatif (B + D); kita tidak bisa menghitung korelasi. Pendekatan ini memiliki beberapa daya tarik. Ini menggunakan semua informasi yang tersedia dan perbedaan jumlah selalu dapat dihitung. Sebaliknya, koefisien tidak didefinisikan jika tidak ada entri dalam satu baris atau dalam satu kolom. Selain itu, indeks (A + D) – (B + C) akan berkorelasi positif dengan koefisien pada kasus-kasus ketika kedua indeks dapat dihitung. Namun, perbedaan menarik tetap ada. Seperti disebutkan di atas, ketika kita mulai dengan distribusi seperti A = 10, B = 5, C = 5, D = 0, peningkatan A atau peningkatan D dengan jumlah yang sama akan meningkatkan selisih skor dengan jumlah yang sama. Sebaliknya, koefisien menjadi lebih positif lebih kuat ketika sel yang lebih kecil dari keduanya ditingkatkan. Either way, kita tidak perlu terlalu khawatir bahwa indeks yang mengintegrasikan semua 4 sel tidak memiliki arti psikologis. Setidaknya kita akan berada di perusahaan yang baik dari semua psikolog yang mengajukan pertanyaan seperti "Semua hal dipertimbangkan, seberapa bahagiakah Anda?" Pertanyaan-pertanyaan semacam itu mengasumsikan bahwa responden dapat mengambil stok pengalaman yang relevan, mengambil sampel dari ingatan, dan membuat penilaian atas penyimpangan mereka secara keseluruhan.

Karena itu, dan ini adalah pelajaran yang kita pelajari dari Einhorn, kita dapat menanyakan apa yang terjadi ketika responden hanya mempertimbangkan sebagian dari informasi yang dapat diakses — yaitu, jika mereka gagal melihat keempat sel skema. Responden biasa tidak sendirian dalam keberpihakan mereka. Beberapa psikolog 'positif' menyarankan kita untuk menghitung berkah kita — yaitu, untuk fokus pada kesenangan di sel A. Yang lain, dari aliran hedonisme, bertanya tentang keunggulan relatif kesenangan atas rasa sakit (yaitu, A – C). Yang lain lagi, dari aliran kepuasan-keinginan, bertanya tentang lebih banyak keinginan yang terpenuhi daripada keinginan yang digagalkan (A – B). Wawasan Einhorn adalah bahwa semua upaya ini datang dengan titik buta yang unik, dan semua berbagi titik buta dalam mempertimbangkan apa yang tidak kita miliki tetapi juga tidak kita inginkan. Jadi, atas dasar konseptual dan statistik, sel D penting.

Namun, sebagai konjungsi dari dua negatif (tidak mau & tidak punya), sel D seperti hantu. Itu mudah diabaikan, tetapi ketika kita menghadapinya tanpa disadari, itu cenderung menakuti kita. Di hari yang baik, perenungan sel D bisa melahirkan humor, wawasan, dan kebijaksanaan. Diagoras dari Melos dikatakan telah mengunjungi kuil dewa laut yang melindungi para pelaut. Ketika tuan rumahnya senang dengan banyak persembahan nazar yang dibuat oleh para pelaut yang telah kembali dengan selamat ke pantai, Diagoras mencatat bahwa akan ada lebih banyak persembahan jika para pelaut yang tenggelam juga memiliki kesempatan untuk berterima kasih kepada para dewa (Pettigrew, 1998). Kisah lain dari zaman kuno membuat intinya lebih langsung. Dalam De Rerum Natura, penyair Lucretius merenungkan 'Betapa indahnya, ketika angin menerpa laut besar menjadi gelombang besar yang menimpa para pelaut, untuk menatap dari daratan kering pada kesengsaraan orang lain. . . [ayat pembuka Buku II; Ramah, mari magno turbantibus. . .] (Slavitt, 2008; lihat juga Krueger, 2021). Itu sel D! Tentu saja, sel D dapat direnungkan tanpa melihat penderitaan orang lain. Ini adalah sikap yang kurang jahat, dan itu tidak akan membawa rasa bersalah yang selamat di belakangnya.

Skema Einhorn adalah skema umum. Ini dapat diterapkan pada domain kehidupan apa pun. Robyn Dawes (2006), seorang psikolog kognitif terkemuka, kritikus psikologi klinis, dan kontemporer Einhorn, menangkap masalah dalam karyanya tentang bias ketersediaan struktural. Psikolog klinis, Dawes berpendapat, cenderung menderita ilusi validitas karena mereka tidak memiliki pengetahuan tentang individu yang tidak mereka obati tetapi yang menjadi lebih baik (ini mungkin sel B). Kemudian lagi, psikolog ini juga kurang pengetahuan tentang mereka yang tidak mereka tangani dan yang tidak sembuh (sel D). Memikirkan kasus-kasus itu mungkin membantu para psikolog ini untuk melunakkan pukulan kritik Dawes.

Sebagai seorang blogger, saya (JK) bisa memikirkan semua postingan keren yang saya tulis. Saya juga bisa memikirkan hal-hal baik yang belum bisa saya tulis dan yang ternyata buruk atau dikritik dengan kasar oleh para komentator (ketika situs masih mengizinkan komentar). Mengikuti Einhorn, sekarang saya akan duduk dan merenungkan tulisan-tulisan yang tidak pernah ingin saya tulis dan tidak pernah saya tulis. Itu akan membuatku merasa lebih baik. Sebagai seorang blogger, saya (JK) bisa memikirkan semua postingan keren yang saya tulis. Saya juga bisa memikirkan hal-hal baik yang belum bisa saya tulis dan yang ternyata buruk atau dikritik dengan kasar oleh para komentator (ketika situs masih mengizinkan komentar). Mengikuti Einhorn, sekarang saya akan duduk dan merenungkan tulisan-tulisan yang tidak pernah ingin saya tulis dan tidak pernah saya tulis. Itu akan membuatku merasa lebih baik.

Lokasi:

Berbagi :